Abstract
A major trust of modal parameters identification (MPI) research in recent years has been based on using artificial and natural vibrations sources because vibration measurements can reflect the true dynamic behavior of a structure while analytical prediction methods, such as finite element models, are less accurate due to the numerous structural idealizations and uncertainties involved in the simulations. This paper presents a state-of-the-art review of the time-frequency techniques for modal parameters identification of civil structures from acquired dynamic signals as well as the factors that affect the estimation accuracy. Further, the latest signal processing techniques proposed since 2012 are also reviewed. These algorithms are worth being researched for MPI of large real-life structures because they provide good time-frequency resolution and noise-immunity.
1. Introduction
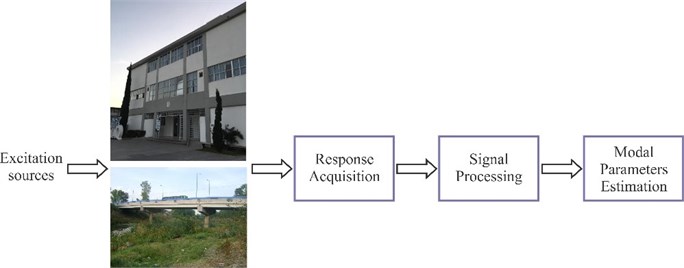
In the past two decades, modal parameters identification (MPI) has become a significant and growing research discipline in several areas such as aeronautics, mechanical engineering, and civil engineering because it can be used to assess the health of the structure and control its vibrations during dynamic events such as an earthquake. For civil structures, it can also be used to satisfy the seismic demands during ground motions in the form of response spectrum analysis. In general, MPI consists of three main steps: excitation and acquisition, signal processing, and modal parameters estimation, such as natural frequencies, damping ratios, and mode shapes (As seen in Fig. 1).
A major trust of MPI research in recent years has been based on using artificial and natural vibrations sources because vibration measurements can reflect the true dynamic behavior of a structure while analytical prediction methods, such as finite element models, are less accurate due to the numerous structural idealizations and uncertainties involved in the simulations. MPI based on vibration data represents a challenge because measured data is non-stationary and is embedded in high-level noise. Furthermore, closely-spaced modal parameters found in a structure due to symmetric geometries or similar physical properties in different directions represent an additional challenge to MPI schemes [1]. For these reasons, it is of paramount importance to have an accurate signal processing algorithm capable of estimating the modal parameters of a civil structure using signals that are non-stationary with a high-level of noise and possibly closely-spaced modes.
Fig. 1Main steps in MPI
Sirca Jr. and Adeli [2] present a review of the strategies used to perform structural system identification. Amezquita-Sanchez and Adeli [1] present an extensive review of signal processing techniques to extract features from the acquired vibrations signals for the purpose of structural health monitoring. This paper presents a state-of-the-art review of journal articles on time-frequency techniques for vibration-based MPI. The focus is on civil structures including high-rise buildings and bridges. The rest of the paper is organized as follows. First, the excitation source and the effect of temperature on MPI accuracy is discussed. Next, vibration-based time-frequency techniques used for MPI as well as their advantages and disadvantages are presented. Then, novel signal processing techniques that are potential candidates to be utilized in MPI schemes are presented. The article ends with some final remarks.
2. Influence of the excitation source and the temperature effect on the MPI accuracy
The excitation source and environmental temperature influence the MPI accuracy significantly. For instance, if a small excitation force is applied to the structure, the measured response might not reflect the full behavior of the structure. Furthermore, the acquired dynamic signals could contain mostly noise or the useful information might be embedded in a high-level of noise. In contrast, a large excitation force can produce damage in the structure. On the other hand, the environmental temperature can modify the mechanical properties of the materials used in the structure thus producing changes in the identified modal parameters.
Different kinds of excitation sources have been used in vibration-based MPI research. The most common ones are reviewed and their advantages and disadvantages are pointed out in this section. Further, the main effects produced by environmental temperature on the MPI accuracy as well as possible solutions to overcome them are addressed.
2.1. Excitation source
The excitation source is an important step in the MPI of a civil structure as it induces energy into the structure in form of vibrations to be monitored to observe its dynamic behavior. To perform this task, artificial and natural or ambient forces have been used to excite civil structures. Artificial excitations are generated by using a man-made mechanical equipment such as drop weights, hammers, and shakers, among others; however, an easy access to the structure and its temporary closing during the test are required [3] which may not be possible for certain structures such as a residential condominium building. Consequently, a significant part of MPI research has focused on natural excitations or ambient vibrations such as wind, micro-earthquakes, and traffic loadings since this type of excitation requires neither excitation equipment nor the interruption of the structure’s normal operation.
In general, the use of artificial or natural excitations depends on the nature of the structure under study and the available budget for testing. For example, if the structure has a relatively small size, the cost and complexity of mechanical equipments to generate the artificial vibrations are lower than those required for large structures. In the latter case ambient vibrations are preferred since they are capable of exciting a large structure without requiring sophisticated mechanical equipments. In addition, they allow the monitoring of the structure under real operating conditions. Moreover, they are useful in providing information in the low-frequency band (below 1 Hz) because mechanical and electrical components used in the artificial exciters cannot reproduce them easily [4]. On the other hand, if high-frequency information is required, artificial exciters are recommended since the frequency range can be adjusted by controlling some features of the exciter [4]. In both cases, it is worth noting that if the energy injected in the structure is small, the structure will not be excited correctly and the measured dynamic signals will only contain noise; on the contrary, if the excitation is too high, the structure can suffer damage [5]. Table 1 presents a comparison of artificial and natural sources for exciting civil structures.
Table 1Comparison of artificial and natural sources for exciting civil structures
Excitation source | Cost | Frequency Content | Availability | Ease of use | Real-time assessment |
Artificial | Depends on the structure size | Broadband | Depends on the mechanical equipment | Depends on the mechanical equipment | No |
Natural | Free | Low Frequency | Always | Easy | Yes |
2.2. Environmental temperature effects on the MPI accuracy
Temperature can produce changes in the physical properties of the materials used in the structure. For instance, an increase in the temperature results in an increase in the material length thus producing a decrease in the structure stiffness. Furthermore, temperature variations may cause changes in the boundary conditions thus affecting the modal parameters values [6].
In recent years, researchers have proposed various schemes to quantify and compensate for the effects of temperature in the modal parameter values. Xia et al. [7] show that modal frequencies, in particular the first modal frequency, are affected greatly by the change of temperature, but not the damping ratios and modal shapes. They examine and compare three methods: linear regression (RM) models, blind source separation (BSS) models [8], and autoregressive (AR) models to compensate the temperature effects in a steel truss girder suspension bridge and a reinforced concrete (RC) high-rise building and conclude that the RM algorithm allows compensating for the temperature effects on the modal frequencies when the structure behaves linearly, but when the relationship is slightly non-linear, the AR and BSS algorithms have an edge for compensating the temperature effects on the modal frequencies. The AR, however, cannot model complex problems such as complicated nonlinear behavior of civil structures and noise-contaminated measured structural response which is usually the case [1].
To model the nonlinear relation between the temperature and modal parameters, Nandan and Singh [9] propose a subspace system identification-based approach, combined with input data filtering to model the temperature–frequency relationship of two realistic bridge configurations: a simply-supported concrete box-girder and a T-beam girder superstructure, located in North Carolina, USA. They use the acquired data from these real-life bridges and note that the data must be filtered before utilization because of the seasonal variation in the data. Laory et al. [10] examine and compare multiple linear regression (MLR), artificial neural networks (ANN) [11, 12], support vector regression (SVR) [13, 14], regression trees (RT) [15], and random forest (RF) [16] algorithms to estimate the natural frequencies of a steel truss bridge under different environmental conditions and conclude that SVR and RF algorithms can be used to model the nonlinear relationship between the environmental conditions and modal parameters. Despite some promising results to compensate for the effects of the environmental conditions in the MPI, the problem has not been completely resolved because of high nonlinearities in the acquired signal. For this reason, it is desirable to investigate new algorithms to model the environmental conditions-modal parameters relationship more appropriately.
In recent years, Adeli and associates have proposed new hybrid approaches for modeling or predicting highly nonlinear systems. Adeli and Jiang [17] present a nonlinear autoregressive moving average with exogenous inputs-based time-delay fuzzy wavelet neural network (WNN) algorithm for system identification of multistory building structures. They use concepts from the chaos theory, wavelets [18], and soft computing techniques, neural networks and fuzzy logic [19, 20], to model the highly nonlinear earthquake-structure system and to incorporate the inherent imprecision of the acquired data. Wang and Adeli [21] present a novel self-constructing WNN for vibration control of nonlinear structures. They integrate a self-constructing WNN with an adaptive fuzzy sliding mode control approach to construct a model that does not need a-priori knowledge of the structure’s dynamics. They test the methodology using a benchmark problem, the finite element model (FEM) model of a continuous cast-in-place pre-stressed concrete box-girder bridge [22]. To the best of the authors’ knowledge, these new approaches have not been reported in the literature to model the environmental conditions-modal parameters relationship. The authors believe that these advanced models have great potentials and their application should be explored for compensating the environmental effects in the modal parameters, especially the modal frequencies.
3. Signal processing techniques for MPI
In real-life structures, the acquired dynamic signals are embedded in different levels of noise. The noise in signals generated using artificial excitations is in general lower than the noise in signals acquired for civil structures excited with ambient sources. This difference requires the utilization of more robust algorithms. Several signal processing techniques have been proposed and used to deal with this type of signals. In this section, the most common ones are reviewed in a chronological order and their advantages and shortcomings are pointed out.
3.1. Time-domain methods
Time-domain methods belong to a class of algorithms that do not require a space transformation (e.g. the frequency domain) to estimate the modal parameters of civil structures.
3.1.1. Statistical time series
Statistical time series models (STSM) use the measured response to establish an approximate mathematical model to represent the acquired dynamic behavior. They are known to be efficient for modeling time-invariant linear systems [1]. They include autoregressive (AR), moving-average (MA), autoregressive with exogenous inputs (ARX), autoregressive-moving-average (ARMA), autoregressive-moving-average with exogenous inputs (ARMAX), and Box-Jenkins (BJ) models.
Takewaki and Nakamura [23] present an experimental analysis to estimate the natural frequencies and damping ratios of a base-isolated three-storey reinforced concrete (RC) building subjected to the 2004 Tokaido-oki, Japan, earthquake using a batch processing least-squares estimation method combined with an ARX model. They show that using the poles (the roots of the denominator) of the estimated ARX model, the modal parameters as well as their variations during the earthquake can be estimated. Gomez et al. [24] use an ARX model to identify the natural frequencies of a three-span curved RC bridge located in California subjected to traffic-induced vibrations and report that higher modes are not detected because the earthquakes excite only the first four modes.
Civil structures are known for having nonlinear and time-variant behavior [25] which makes the linear STSM ineffective for modeling their dynamical behavior because they can model only time-invariant systems thus limiting an accurate estimation of the modal parameters. To lessen this drawback, Maosheng et al. [26] combine a recursive adaptive forgetting factor with an ARX model for MPI of the scaled model of 12-story RC frame structure subjected to the 1940 El Centro earthquake. The model detects the response of the structure when the response is time-invariant where the modal parameters are estimated from the entire acquired response using the poles of the ARX model. In contrast, when the response is time-varying, the model identifies the instance when the signal changes abruptly in amplitude. Once the change is detected, the previous samples are used to estimate the modal parameters using the poles of the ARX model. Su et al. [27] present a time-varying ARX (TVARX) model to estimate the instantaneous modal parameters through integration with wavelets and apply it to two 2D structures, a five-story and an eight-story steel frame subjected to the 1999 Chi-Chi, Taiwan earthquake. They report an identification error of about 2 % and 20 % for the natural frequencies and damping ratios, respectively. Other applications of statistical time series have been reported by Saito and Beck [28] and Niu et al. [29].
In statistical time series method, in general, the model order selection is a key to the accurate estimation of modal parameters. This selection is made either by a trial-and-error or an adaptive approach. The trial-and-error approach is time-consuming and impractical. Consequently, other alternatives should be explored. For instance, Saito and Beck [28] use a Bayesian approach for identifying the best order for the ARX model used for estimating the MPI of a high-rise building.
3.1.2. Free decay-based methods
When a civil structure is excited by a hammer or a drop-weight, the free-decay response of the structure is measured. The term free is used because the excitation forces used can be treated as impulses. However, in real-life, the impulse excitation is seldom utilized because it cannot excite large civil structures adequately. Therefore, techniques such as the random decrement technique (RDT) [30] or the natural excitation technique (NExT) [31] are proposed to transform the response acquired by another type of excitation such as ambient or man-induced vibrations into a free-decay response.
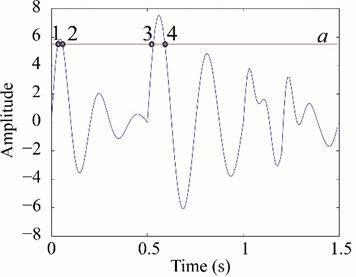
RDT aims to convert the acquired signal into a free-decay response by averaging segments of the acquired response with a common initial condition using a given threshold [32]. A graphical illustration of the method is shown in Fig. 2. A threshold value () is used for obtaining the samples that fulfill the aforementioned condition (Fig. 2(a)). This value is obtained using the level crossing condition [33]:
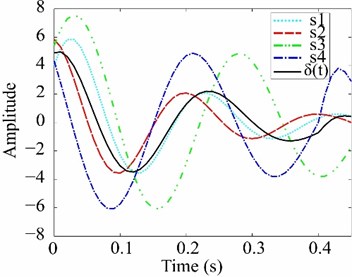
where is the signal standard deviation. Then, a segment of equal sample length (the curves labeled as s1, s2, s3, and s4) is extracted for every sample that satisfies the aforementioned condition (Fig. 2b). The resulting signal () is obtained as [34]:
where is the number of obtained segments, and can be treated as the structure’s free-decay response. He et al. [35] use the RDT algorithm to calculate the MPI of a three-span continuous steel truss bridge subjected to ambient vibrations produced by a moving train. The modal parameters are obtained iteratively solving a set of non-linear equations formed using the free-response equation. The results obtained are compared with the peak-picking (PP) method. They conclude that RDT estimates the first four modes whereas PP identifies only the first three. Other applications of RDT for MPI are presented by Cury et al. [36] and Wang and Chen [37].
Despite good results reported in the aforementioned works, some unresolved difficulties remain using the RDT technique. RDT should be used with stationary or quasi-stationary signals as any slight variation can cause a change of the free-decay signal amplitude, leading to miscalculation of the damping ratio since a higher damped signal is estimated by the algorithm [38]; but, the measured signals obtained for real-life structures from dynamic excitations exhibit nonlinear and non-stationary properties. In order to overcome this limitation, Lin and Chiang [39] present a modified RDT technique combined with the Ibrahim time domain (ITD) method [40] to estimate the modal parameters of a 2D 3-bay 17-member cantilever space truss subjected to band-limited noise as excitation. They report identification error of less than about 1 % and 20 % for the natural frequencies and damping ratios, respectively. Lin and Tseng [41] use RDT with a time-varying threshold value on a 6-degree-of-freedom model with viscous damping and an added 10 % noise. They report maximum errors in the natural frequencies and damping ratios of 1 % and 18 %, respectively.
Fig. 2RDT estimation
Unlike RDT technique, the NExT technique obtains the free-decay response of a signal either by applying directly the cross correlation function to the signal or using the FFT (FFT is used only to obtain the cross-correlation function) and its inverse to calculate the cross-spectral density function [42]. Several applications of the NExT technique combined with the eigensystem realization algorithm (ERA) [43] have been reported for finding the MPI of a 1/40 scale cable-stayed bridge [44], suspension bridges [45], a two-span continuous steel frame footbridge [46], a 16-bay truss structure [47], Masonry Monuments [48, 49], and a Langer-type arch steel bridge [50].
A major drawback of the NExT method is its increased computational burden in comparison with RDT. In order to lessen this problem, Chang and Pakzad [51] propose an enhanced NExT algorithm to estimate the modal parameters of the Golden Gate Bridge located at San Francisco, California, USA. A wireless sensor network is used to measure its response when it is subjected to ambient vibrations. They report maximum errors of about 1 % and 23 %, for the estimation of the natural frequency and damping ratio, respectively.
3.1.3. Subspace methods
Stochastic subspace identification (SSI) algorithms are another class of time-domain methods for estimating the modal parameters of civil structures subjected to ambient dynamic vibrations [52]. Different types of SSI methods have been proposed such as covariance-driven SSI (SSI-COV) [53], covariance-variate SSI (SSI-CV) [54], and data-driven SSI (SSI-DATA) [55]. Van Overschee and De Moor [52] show that all SSI methods can be generalized into a unified theory depending on the weighting matrix selection before the numerical decomposition. A review of the aforementioned methods is presented by Peeters and De Roeck [56].
SSI has been used to estimate the modal parameters of steel footbridges [57, 58], cable-stayed footbridges [59], a stone arch bridge [60], a stress-ribbon footbridge [61], suspension bridge [62], a highway RC bridge [63], RC buildings [64], a super high-rise tower [65], and masonry buildings [66].
SSI algorithms in general present high immunity to noise in the signals [65], but are computationally intensive, requiring significant computational resources especially for large structures [67, 68]. Furthermore, they cannot estimate closely-spaced modes accurately because they require setting the order or number of modes which can produce an underdetermined or overdetermined system. If the former model is set, some modes would not be detected, whereas the latter could produce spurious modes [57, 68, 69]. In order to lessen some of the problems found in the SSI methods, Reynders et al. [70] propose a modification to the SSI algorithm based on using both the measured responses from the ambient vibrations and the ones obtained with an artificial exciter to perform the MPI of a steel footbridge subjected to ambiental vibrations and artificial excitations. They show an improvement in the quality of the estimation of the modal parameters. Zhang et al. [68] introduce a modification to the SSI-DATA algorithm in order to reduce its computational burden and apply it to a suspension bridge subjected to ambient excitations. The original SSI-DATA method uses QR-factorization, the singular value decomposition (SVD), and least squares to determine the modal parameters which is computational intensive. In contrast, the modified method avoids the use of the QR-factorization by employing an eigenvalue decomposition. Further, they propose a similarity index to eliminate the fictitious modes. Li and Chang [67] introduce an optimization scheme for the online operation of the SSI-COV method and test it using the ASCE benchmark frame structure. In this algorithm, QR-factorization is substituted with the Householder bi-iteration subspace tracker, which along the utilization of a state-space constructed subspace, minimizes the required time to compute the modal parameters since only part of the measured signal needs to be used. Their approach can deal with colored noise (noise whose frequency content is not uniform). Hong et al. [69] present an enhanced version of the canonical correlation analysis (CCA) to allow a better detection of the closely-spaced modes and test it using the actual measurements obtained from a suspension bridge subjected to wind excitation.
Another type of subspace method is the proper orthogonal decomposition (POD) (or Karhunen-Loève decomposition). POD allows analyzing multidimensional data. A detailed explanation of this algorithm can be found in [71]. Kallinikidou et al. [72] use POD for MPI of a cable-suspended bridge subjected to traffic-induced vibrations as excitation. POD calculates the modal parameters using the covariance matrices of the bridge measurements at selected locations. The authors conclude that the POD method can deal with a huge amount of data, as only the most relevant sensors are used, allowing its utilization in real-time structural health monitoring (SHM) schemes. Wang and Cheng [73] propose a modification for calculating non-proportional damping ratios using POD. They test the methodology employing a steel cantilever beam subjected to a band-limited excitation. They identify the natural frequencies with high accuracy, as a maximum deviation of 2 % is achieved; but, the error for the estimation of the damping ratio is over 50 % compared with the theoretical values.
3.2. Frequency-domain methods
Unlike time-domain methods, frequency-domain approaches must use a space transform in order to identify the existent components of the measured signal and estimate the modal parameters. This class of algorithms is known for their ease-of-use. In some cases, the required computational burden is lower than that of the time-domain methods. The most widely-used algorithms are discussed in this subsection.
3.2.1. Fourier Transform-based methods
Fourier Transform (FT) is one of the well-known and most popular algorithms used to identify relevant information in the frequency domain. In MPI applications, the optimized discrete version, known as the Fast Fourier Transform (FFT) is the one chosen for implementation on personal computers (PC) and portable platforms such as digital signal processors (DSP), microcontrollers, and field programmable gate arrays (FPGA). FFT has been used to estimate the natural frequencies of 12-, 19-, and 23-story RC building structures [74], and a prestressed RC bridge [75]. Valla et al. [76] calculate the natural frequencies of two 30-storey RC buildings subjected to ambiental vibrations employing the FFT.
In the last two decades, different algorithms based on the FFT such as peak-picking (PP) method, frequency domain decomposition (FDD) [77], and frequency response function (FRF) have been proposed to estimate the modal parameters of civil structures subjected to dynamic vibrations. Proposed by Bendat and Piersol [78], the PP method uses FFT to obtain the signal amplitude spectrum where the natural frequencies are the highest peaks of the spectrum, and the damping ratios are calculated using either the half-power bandwidth or the logarithmic decrement methods while the mode shapes are estimated using SVD. The FDD method is based on the decomposition of the power spectral density matrix using the SVD method to estimate the modal parameters of the structure [77], whereas the FRF method uses the Fourier transform of the input excitation and the measured response to estimate a transfer function which is used for calculating the modal parameters of a civil structure [32].
Several examples of PP, FDD, and FRF methods for MPI of civil structures have been reported. Li et al. [35] compare the PP, FDD and RDT methods to estimate the modal parameters of a 101-storey office highrise building with five basement levels subjected to the 2008 Shichuan, China earthquake. They use FDD and PP to estimate the natural frequencies, whereas RDT and FDD are employed to compute the damping ratios. García-Palencia and Santini-Bell [79] use the FRF method to estimate stiffness, mass, and viscous damping matrices of a linear elastic damped structure. They conclude that the FRF method does not work well under severe ambient conditions. Erdogan and Gülal [80] apply the PP method to calculate the modal parameters of a suspension bridge subjected to ambient dynamic vibrations and conclude that only lower modes can be identified.
Although FDD improves the resolution of PP by using the SVD method, the selection of the frequencies still remains as a manual task which can be a time-consuming procedure [81]. In order to lessen this problem, Gade et al. [82] propose a modified version of FDD method known as enhanced FDD (EFDD) method which automates the process of identifying the natural frequencies by using a zero-crossing criteria. Furthermore, the inverse discrete Fourier transform is used to extract the individual mode and to estimate the modal parameters. Altunisik et al. [83] compare the SSI and EFDD methods for estimating the modal parameters (natural frequencies and damping ratios) of a box girder bridge subjected to traffic as excitation source. They report both algorithms estimate similar values. Other similar works have been presented by Magalhães et al. [84], Soyoz et al. [85], and Cismaşiu et al. [86], among others. Another modification of the original FDD method is the frequency spatial domain decomposition (FSDD) [87] which uses spatial filtering to improve the estimation of modal frequencies and damping ratios.
FFT and its derived algorithms present significant limitations. They cannot be used for estimating the modal parameters of structures subjected to ambient dynamic excitations because the monitored signals in a structure exhibit nonlinear and non-stationary properties which cannot be modelled by FFT adequately [1]. In order to lessen the limitation of FFT, Agneni et al. [88] propose a Hilbert transform (HT)-based algorithm for obtaining the FRFs.
3.2.2. High-resolution methods
High-resolution (HR) methods are known for detecting frequencies, especially closely-spaced ones, in signals with a low signal-to-noise ratio (high-level noise) [89]. Among the HR methods, the multiple signal classification (MUSIC) [90] has been used to estimate the natural frequencies of civil structures. Jiang and Adeli [89] present a MUSIC method to estimate the pseudospectrum of high-rise buildings subjected to artificial vibrations created by a shake table. The estimated frequencies are used to construct a damage indicator. The authors were the first to use the MUSIC approach in the field of structural engineering. Osornio-Rios et al. [91] employ MUSIC for calculating the natural frequencies of a five-bay truss-type structure subjected to artificial vibrations. The natural frequencies are used as inputs to a classifier to detect and quantify the damage severity. Amezquita-Sanchez et al. [92] compute the natural frequencies of a five-bay truss structure with 70 members using the MUSIC method. They show that closely-spaced modes can be estimated. The pseudospectrum calculated by MUSIC cannot be used for estimating the damping ratio because its amplitudes have no physical significance, which is the opposite to the FFT spectrum. For this reason, other methods must be explored to obtain the damping ratio values [93].
None of the techniques discussed so far can determine the instantaneous changes or the evolution over time of the modal parameters. If those features are required, time-frequency methods must be used.
3.3. Time-frequency methods
These methods combine the properties of both time and frequency methods to provide an enhanced detectability of frequencies, especially closely-spaced ones. This subsection presents the main algorithms used in MPI schemes.
3.3.1. Wavelet transform
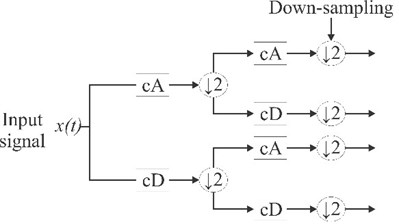
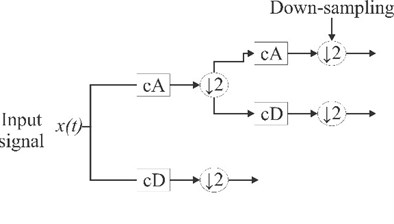
During the last two decades, wavelet transform (WT) has become the most widely-used time-frequency algorithm for signal processing in different engineering applications such as seismic engineering [94], filtering approaches [95], structural control [96-98], structural reliability analysis [99, 100], pavement structural evaluation [101], damage detection [102], and biomedical signal processing [103, 104] because it provides a multi-resolution time-frequency analysis, allowing the detection of sudden frequency changes, transients, and other features that are invisible in time domain [105]. The continuous wavelet transform (CWT), discrete wavelet transform (DWT), and wavelet packet transform (WPT) have been the most widely-used methods. The main difference between CWT and DWT is how the shifting and scaling is performed. DWT estimates the WT using dyadic blocks, whereas CWT does not, that is, the rates used in the aforementioned processes are chosen by the final user. Fig. 3 shows the decomposition tree for DWT and WPT where it seen that WPT decomposes both detail coefficients (dC) and approximation coefficients (aC) (Fig. 3(a)), whereas DWT decomposes only the aC (Fig. 3(b)). In this regard, it is seen that WPT is an improvement to DWT to allow the extraction of individual frequencies.
Fig. 3Tree decompositions for a) WPT and b) DWT
a)
b)
In recent years, WT has risen as an important signal processing tool for MPI of different civil structures. Ülker-Kaustell and Karoumi [106] examine the Morlet CWT for MPI of a concrete-steel composite railway bridge subjected to ambient dynamic vibrations caused by moving trains. The amplitude and phase of extracted signals are used to calculate the natural frequencies and damping ratios. They conclude that the values of the identified natural frequencies decrease and the damping ratio increases when the train increases its speed and vice versa. Le and Paultrec [107] apply CWT and the Cauchy wavelet to estimate the natural frequencies and damping ratios of a full scale two-storey RC building subjected to band-limited noise as excitation. The authors report that the method can identify closely-spaced modes. Kim and Chen [108] examine WPT to estimate natural frequencies and damping ratios of a linear three-degrees-of-freedom vibration system and report that the modal parameters of the simple system can be estimated with accuracy.
WT-based approaches have some drawbacks. For example, DWT method lacks translation-invariance which can affect the estimation of the modal parameters. In order to lessen this problem, Holschneider et al. [109] propose the stationary WT (SWT) which achieves translation-invariance by removing the down-samplers and up-samplers in the DWT and up-sampling the filter coefficients by a factor of in the -th level of the algorithm [110]. Sadhu et al. [111] examine SWT algorithm for computing the modal parameters of a 15-story steel-frame building subjected to ambient dynamic vibrations. SWT is used to decompose the time signal into several frequency bands, where the modes are calculated by using the parallel factor tool. Su et al. [112] apply the SWT algorithm to compute the modal parameters of an 8-story steel frame and a steel box girder cable-stayed bridge subjected to band-limited noise and ambient dynamic vibrations, respectively. They report maximum accuracies of 2 % and 20 % for the natural frequencies and damping ratios, respectively.
The aforementioned WT algorithms have a fixed resolution which might require the utilization of other signal processing techniques such as EMD-based methods to fully extract the individual modes. In order to overcome these limitations, Daubechies et al. [113] proposed the Synchrosqueezed Wavelet Transform (SQWT) as a new adaptive WT capable of working with signals with high-level of noise. To test the effectiveness of the SQWT, Perez-Ramirez et al. [93] apply the SQWT and the Gaussian wavelet to estimate the natural frequencies and damping ratios of a scaled 3D four-story two-bay by two-bay steel-braced frame subjected to ambient dynamic vibrations. The results indicate the modal parameters of both structures are estimated with high accuracy, especially the closely-spaced modes.
3.3.2. Hilbert-Huang transform
Huang et al. [114] introduced the empirical mode decomposition (EMD) combined with Hilbert transform (HT) known as Hilbert-Huang transform or HHT as an adaptive signal processing method capable of analyzing stationary, nonlinear, non-stationary, and transient signals. The EMD method decomposes any time series data into a set of band-limited quasi-stationary functions, called intrinsic mode functions (IMF). Next, the HT is applied to each IMF to obtain its amplitude and phase angle, which are used to estimate the natural frequencies () and damping ratios () of a civil structure using the following equations:
where and are the phase and amplitude of each IMF, respectively. Fig. 4 illustrates the application of HHT to calculate the natural frequencies and damping ratios of a synthetic signal generated using the following equation [115]:
where the signal is composed of two modes whose frequencies () are 20 and 50 Hz, respectively, the damping ratios () are 1 % and 0.5 %, respectively, and the amplitudes () are 1.0 for every mode (Fig. 4(a)). The test signal is not corrupted with noise [0] and the phase () for every mode is 0. The sampling frequency used is 1000 Hz, during 2 s, to obtain 2000 samples. Fig. 4(b) illustrates the individual components extracted using EMD, whereas Fig. 4(c) depicts the modal parameters estimated using HT showing their evolution over time. HHT method has been applied in different fields such as biomedical engineering [116], mechanical engineering [117], and earthquake engineering [118].
Fig. 4MPI estimation using HHT: a) a sample test signal, b) individual modes, and c) the estimated natural frequencies and damping ratios.
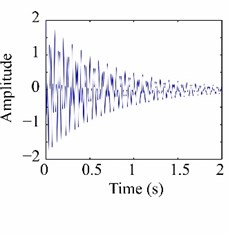
a)
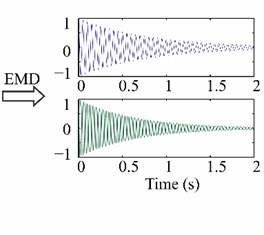
b)
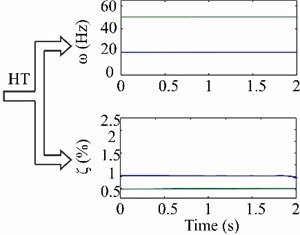
c)
Shi et al. [119] compare the HHT and PP methods for estimating the modal frequencies and damping ratios of the 101-story Shanghai World Financial Center subjected to ambient dynamic vibrations. The results show both methods estimate similar values for the natural frequencies but HHT is more accurate than PP for estimation of the damping ratios. Ditommaso et al. [120] compare the HHT, STFT, and the S-Transform (ST) for identifying the natural frequencies of a brick-masonry bearing wall structure subjected to the vibrations created from the explosion of a World War II bomb. They conclude that ST allows following the time evolution of the natural frequencies detected, especially for the higher ones. On the other hand, they report that HHT does not have the expected performance. They point out that some of the high-frequency modes extracted using EMD contain low-frequency information, known as mode-mixing effect, this impeding its application to MPI.
A major problem of the HHT method is the mode-mixing effect encountered in the EMD process which means that waves with the same value of frequency are assigned to different IMFs in the sifting process [121]. Different strategies have been proposed in recent years in order to lessen this undesirable effect. Pai et al. [122] modify the EMD process by coupling it with the conjugate-pair decomposition (CPD) method in order to detect if the IMF has two different frequencies or not. If they have, the CPD method is used to further decompose the IMF. They use the method to estimate the modal parameters of three damped modes of a horizontally cantilevered steel beam subjected to an initial tip displacement and report better performance than the EMD method when dealing with transient and noisy signals.
3.3.3. Blind source separation
Blind Source Separation (BSS) is a non-parametric algorithm capable of recovering the original sources from a mixture of signals [8, 123]. An explanation of the algorithm is presented in a recent article by Amezquita-Sanchez and Adeli [1]. The most known BSS algorithms are the independent component analysis (ICA) [124], and the second-order blind identification (SOBI) [125]. The former assumes that the measured data is a linear combination of statistically independent sources. On the other hand, the latter uses the sources temporal structure [126].
Poncelet et al. [126] evaluate the performance of ICA and SOBI methods to estimate the modal parameters of a 3-DOF model and report that ICA can process signals from weakly excited systems, whereas SOBI can also handle signals obtained from moderately damped systems. A shortcoming of SOBI is its inability to identify closely-spaced modes [127]. Hazra et al. [127] propose a hybrid time-frequency approach based on SWT and EMD to alleviate the limitation of SOBI. The method also solves the under-determined case (the number of acquired sensors is fewer than the number of modes to be identified). They carry out the MPI of a 10-story steel tower with a composite steel deck subjected to ambiental vibrations. Yang et al. [128] modify the ICA algorithm to detect moderate damping modes and apply it to a cantilever beam excited with an impact hammer. They show the method can estimate modes whose damping ratio does not exceed 1 %.
3.4. Probabilistic methods
In recent years, probabilistic methods (PM) have become an important signal processing tool to estimate the modal parameters of civil structures using incomplete data. Cara et al. [129] use the Expectation-Maximization (EM) fused with the maximum likelihood estimation (MLE) methods and SSI-DATA to compute the natural frequencies and damping ratios of a four-story two-bay by two-bay braced steel frame subjected to ambient dynamic vibrations. Although the method can estimate the natural frequencies accurately, the damping ratio values show large variances to their theoretical counterparts.
Bayesian probability has been explored the most to identify the modal parameters of civil structures because it can deal with the unavoidable uncertainties of the measured data. Cheung and Beck [130] propose a Bayesian-based methodology to estimate the modal parameters using the numerical response of a ten-story shear frame with non-classical damping. They point out that the computational burden required for Bayesian-based estimators is high. To overcome this limitation, Au [131] proposes a fast Bayesian FFT-based algorithm to estimate the modal parameters and apply it to the measurements of a 15-story steel-frame subjected to ambient vibrations. The method focuses on detecting well-spaced modes. Yan and Katafygiotis [132] presents a Bayesian approach for estimating the MPI using the statistical properties of the auto-spectral density sum and the statistical information of the spectral density matrix and apply it to a 3-story building structure made of aluminum subjected to horizontal and torsional vibrations generated by a shake table.
3.5. Advantages and disadvantages of the signal processing techniques used in MPI.
The knowledge about the features (e.g. frequency resolution or noise immunity) of the different MPI schemes allows the selection of the appropriate algorithm. An incorrect selection of the algorithm may lead to unreliable results. Table 2 presents a summary of the main advantages and drawbacks of the signal processing techniques used for MPI.
4. Novel signal processing techniques
Recent advances in mathematics and signal processing fields have led to the development of novel algorithms for performing time, frequency, or time-frequency analyses. In this section, some of these algorithms are reviewed. To the best of the authors’ knowledge, these algorithms have not been used for MPI. They have features that make them potential candidates to be employed for the MPI.
Table 2Advantages and disadvantages of the signal processing techniques used in MPI of civil structures
Method | Advantages | Disadvantages |
STSM | Straightforward use. Modal parameters can be directly obtained from the model. Can deal with small noise-level signals. | Linear and stationary model. Accuracy depends on the level of noise. Model order selection can be a time-consuming procedure. |
Free-decay methods | Filtering properties. Can process raw ambiental responses. Simplicity. Easy implementation. | Multi-stage schemes. Increased computational burden. Sensitive to noise. Used mainly to process stationary responses. |
SSI methods | Noise immunity. Closely-spaced modes detection. Modal parameters are directly obtained. Can process slightly non-stationary signals. | Heavy computational burden. Require calibration. Generation of spurious modes. |
FT-based methods | Straightforward use. Modal parameters are directly obtained. Simplicity (PP). Non a-priori knowledge of the number of modes is required. Filtering properties (FRF). | Fixed resolution. Can deal with only stationary signals. Sensitive to noise. Closely-spaced modes are not detected. The input excitation should be available for FRF estimation. If the excitation source is a harmonic signal, the estimated natural frequency can be biased (FDD). |
High-resolution methods | Noise immunity. Closely-spaced modes can be detected. | Computational burden. Require calibration. |
HHT and its variants | Adaptive method. Straightforward use. The individual modes are extracted. No user interaction is required. | Mode-mixing. EMD variants require calibration. Its computational burden and accuracy depends on selected algorithm: EMD (lower), ensemble EMD (higher). |
BSS | Good accuracy to separate frequency components. Can identify modes with low energy. | A pre-filtered stage is required for signal embedded in high-level noise. High damping ratios cannot be accurately estimated. |
Probabilistic methods | Closely-spaced mode detection. A-priori knowledge can be incorporated. Can process noise-corrupted and incomplete data. | High computational burden. Requires calibration. |
4.1. Local characteristic-scale decomposition
As mentioned earlier, the EMD algorithm suffers from the so-called mode-mixing effect which impedes the accurate identification and extraction of closely-spaced modes [1]. In order to lessen this limitation, recently Zheng et al. [133] proposes a new method called Local Characteristic-scale Decomposition (LCD). It uses the concept of mono-component intrinsic scale component (ISC), the equivalent of the IMF in EMD. The main difference between an ISC mode and an IMF mode is that the latter also uses a criterion in order to ensure the smoothness and symmetry of the potential mode. In addition, LCD uses a threshold-based criterion to mitigate the end effect and the mode-mixing issues. The authors used LCD to detect faults in rolling bearings [133] where the mode-mixing and end effect issues have been reportedly alleviated.
4.2. Compact empirical mode decomposition
Proposed by Chu et al. [134], compact empirical mode decomposition (CEMD) is another time-frequency algorithm proposed to overcome the EMD limitation. It uses a criterion to identify false extrema points and a set of algebraic equations to set the upper and lower envelopes using Hermitian polynomials. These features reduce the mode-mixing effect and improve the IMF extraction quality, as the end effect (distortions in the beginning and the end of the component) is corrected.
4.3. MUSIC-Empirical Wavelet Transform
Empirical Wavelet Transform (EWT) is an adaptive wavelet transform that uses FT to detect the frequency bands to contain the modes in order to construct an effective wavelet filter bank so that the modes can be retrieved accurately. Unfortunately, FT accuracy is compromised under noisy environments, affecting the EWT results. Recently, Amezquita-Sanchez and Adeli [135] combined MUSIC algorithm with EWT to improve the accuracy of the original EWT. The proposal uses the MUSIC algorithm to estimate the contained frequencies in the signal and build the appropriate boundaries to create the wavelet filter bank. The authors demonstrate the new methodology is efficient for analyzing nonlinear and nonstationary signals embedded in high-level noise thus allowing the detection of closely-spaced modes accurately.
4.4. Novel blind source separation algorithm
The performance/accuracy of BSS-based algorithms degrades in noisy environments. A solution is to use pre-filtering stages in order to denoise the acquired dynamic signal. This solution, however, increases the computational burden of the proposal thus limiting its application for real-time strategies. In order to mitigate this shortcoming, Chui and Mhaskar [136] propose an adaptive harmonic model for performing the BSS of a multicomponent signal. The proposal removes any existent trend that might affect the component’s detection adversely. Then, signal’s components are extracted using signal separators based on a threshold value. The results show that the method can detect closely-spaced modes. Further, the performance in noisy environments is not degraded. These features make the algorithm a potential candidate for its utilization for the MPI.
5. Final remarks
MPI has become a very active area of research in structural engineering because of the evolution and recent advances in new sensors, signal processing algorithms, as well as the enhanced processing capabilities of the new computers. This paper presented an overview of the main signal processing techniques used in MPI.
The signal processing algorithms commonly used in MPI are time, frequency and time-frequency domain. Time-frequency techniques are the most preferred to estimate the modal parameters of civil structures because they allow observing the evolution of the modal parameters over time.
The newest signal processing techniques, LCD, CEMD and MUSIC-EWT, proposed since 2012 have not been used in MPI. These algorithms are worth being researched for MPI of large real-life structures because they provide good time-frequency resolution and noise-immunity, among others.
In spite of the large amount of work presented on MPI, most deal with small and academic problems. New methodologies that use enhanced signal processing techniques capable of handling noisy data and nonlinear signals effectively, accurately, and reliably with computational efficiency for real-time applications should be explored for monitoring the modal parameters of large real-life structures for use in real-time SHM applications.
References
-
Amezquita-Sanchez J. P., Adeli H. Signal processing techniques for vibration-based health monitoring of smart structures. Archives of Computational Methods in Engineering, Vol. 23, Issue 1, 2016, p. 1-15.
-
Sirca G. F. Jr., Adeli H. System identification in structural engineering. Scientia Iranica – Transaction A: Civil Engineering, Vol. 19, Issue 6, 2012, p. 1355-1364.
-
Garcia-Perez A., Amezquita-Sanchez J. P., Dominguez-Gonzalez A., Sedaghati R., Osornio-Rios R., Romero-Troncoso R. J. Fused empirical mode decomposition and wavelets for locating combined damage in a truss-type structure through vibration analysis. Journal of Zhejiang University SCIENCE A, Vol. 14, Issue 9, 2013, p. 615-630.
-
Peeters B., Maeck J., De Roeck G. Vibration-based damage detection in civil engineering: excitation sources and temperature effects. Smart Materials and Structures, Vol. 10, Issue 3, 2001, p. 518-527.
-
He X. H., Hua X., Chen Z., Huang F. EMD-based random decrement technique for modal parameter identification of an existing railway bridge. Engineering Structures, Vol. 33, Issue 4, 2011, p. 1348-1356.
-
Uebayashi H., Nagano M., Hida T., Tanuma T., Yasui M., Sakai S. Evaluation of the structural damage of high-rise reinforced concrete buildings using ambient vibrations recorded before and after damage. Earthquake Engineering and Structural Dynamics, Vol. 45, 2016, p. 213-228.
-
Xia Y., Chen B., Weng S., Ni Y.-Q., Xu Y.-L. Temperature effect on vibration properties of civil structures: a literature review and case studies. Journal of Civil Structural Health Monitoring, Vol. 2, Issue 1, 2012, p. 29-46.
-
Lopez-Gordo M. A., Sanchez Morillo D., van Gerven M. A. J. Spreading codes enables the blind estimation of the hemodynamic response with short-events sequences. International Journal of Neural Systems, Vol. 25, Issue 1, 2015, p. 1450035.
-
Nandan H., Singh M. P. Effects of thermal environment on structural frequencies. Part II – A system identification model. Engineering Structures, Vol. 81, 2014, p. 491-498.
-
Laory L., Trinh N. T., Smith I. F. C., Brownjohn J. M. W. Methodologies for predicting natural frequency variation of a suspension bridge. Engineering Structures, Vol. 80, 2014, p. 211-221.
-
Cabessa J., Siegelmann H. T. The super-turing computational power of evolving recurrent neural networks. International Journal of Neural Systems, Vol. 24, Issue 8, 2014, p. 1450029.
-
Wang L., Liang P. J., Zhang P. M., Qiu Y. H. Adaptation-dependent synchronization transitions and burst generations in electrically coupled neural networks. International Journal of Neural Systems, Vol. 24, Issue 8, 2014, p. 1450033.
-
Castillo E., Peteiro-Barral D., Guijarro Berdinas B., Fontenla-Romero O. Distributed one-class support vector machine. International Journal of Neural Systems, Vol. 25., Issue 7, 2015, p. 1550029.
-
Zhang Y., Zhou W. Multifractal analysis and relevance vector machine-based automatic seizure detection in intracranial. International Journal of Neural Systems, Vol. 25, Issue 6, 2015, p. 1550020.
-
Chou J. S., Pham A. D. Smart artificial firefly colony-based support vector regression for enhanced forecasting in civil engineering. Computer-Aided Civil and Infrastructure Engineering, Vol. 30, Issue 9, 2015, p. 715-732.
-
Donos C., Duemoelmann M., Schulze-Bonhage A. Early seizure detection algorithm based on intractable EEG and random forest classification. International Journal of Neural Systems, Vol. 25, Issue 5, 2015, p. 1550023.
-
Adeli, H., Jiang, X. Dynamic fuzzy wavelet neural network model for structural system identification. Journal of Structural Engineering, Vol. 132, Issue 1, 2006, p. 102-111.
-
Adeli, H., Karim A. Wavelets in Intelligent Transportation Systems. John Wiley and Sons, West Sussex, United Kingdom, 2005.
-
Forero Mendoza L., Vellasco M., Figueiredo K. Intelligent multiagent coordination based on reinforcement hierarchical neuro-fuzzy models. International Journal of Neural Systems, Vol. 24, Issue 8, 2014, p. 1450031.
-
Quiros P., Diaz A. P., Montes S. On the use of fuzzy partitions to protect data. Integrated Computer-Aided Engineering, Vol. 21, Issue 4, 2014, p. 355-366.
-
Wang N., Adeli H. Self-constructing wavelet neural network algorithm for nonlinear control of large structures. Engineering Applications of Artificial Intelligence, Vol. 41, 2015, p. 249-258.
-
Agrawal A., Tan P., Nagarajaiah S., Zhang J. Benchmark structural control problem for a seismically excited highway bridge. Part I: Phase I problem definition. Structural Control and Health Monitoring, Vol. 16, 2009, p. 509-529.
-
Takewaki I., Nakamura M. Temporal variation in modal properties of a base-isolated building during an earthquake. Journal of Zhejiang University – SCIENCE A, Vol. 11, Issue 1, 2010, p. 1-8.
-
Gomez H. C., Ulusoy H. S., Feng M. Q. Variation of modal parameters of a highway bridge extracted from six earthquake records. Earthquake Engineering and Structural Dynamics, Vol. 42, 2013, p. 565-579.
-
Adeli H., Gere J., Weaver W. Jr. Algorithms for nonlinear structural dynamics. Journal of Structural Division, Vol. 104, Issue ST2, 1978, p. 263-280.
-
Maosheng G., Jing S., Lili X. Identification of model structure parameters via combination of AFMM and ARX from seismic response data. Earthquake Engineering and Engineering Vibration, Vol. 13, Issue 3, 2014, p. 411-423.
-
Su W. C., Liu C. Y., Huang C. S. Identification of instantaneous modal parameter of time-varying systems via a wavelet-based approach and its application. Computer-Aided Civil and Infrastructure Engineering, Vol. 29, Issue 4, 2014, p. 279-298.
-
Saito T., Beck J. L. Bayesian model selection for ARX models and its application to structural health monitoring. Earthquake Engineering and Structural Dynamics, Vol. 39, 2010, p. 1737-1759.
-
Niu Y., Fritzen C.-P., Jung H., Buethe I., Ni Y.-Q., Wang Y.-W. Online simultaneous reconstruction of wind load and structural responses – theory and application to canton tower. Computer-Aided Civil and Infrastructure Engineering, Vol. 30, Issue 8, 2015, p. 666-681.
-
Cole H. A. On-the-line analysis of random vibrations. Proceedings of the AIAA/ASME 9th Structures, Structural Dynamics and Materials Conference, Palm Springs, CA, 1968.
-
James G. H. I., Carne T. G., Lauffer J. P. The Natural Excitation Technique (NExT) for Modal Parameter Extraction from Operating Wind Turbines. SAND92-1666 UC-261, 1993, Sandia National Laboratories, Albuquerque, NM.
-
He J., Fu Z.-F. Modal Analysis. Butterworth-Heinemann, Boston, MA, 2001.
-
Rodrigues J., Brincker R. Application of the random decrement technique in operational modal analysis. Proceedings of the 1st International Operational Modal Analysis Conference, Copenhagen, Denmark, 2005, p. 191-200.
-
Ibrahim S. R. Random decrement technique for modal identification of structures. Journal of Spacecraft and Rockets, Vol. 14, Issue 11, 1977, p. 696-700.
-
Li Q. S., Zhi L.-H., Tuan A. Y., Kao C.-S., Su S.-C., Wu C.-F. Dynamic behavior of Taipei 101 Tower: field measurement and numerical analysis. Journal of Structural Engineering, Vol. 137, Issue 1, 2011, p. 143-155.
-
Cury A., Cremona C., Dumoulin J. Long-term monitoring of a PSC box girder bridge: operational modal analysis, data normalization and structural modification assessment. Mechanical Systems and Signal Processing, Vol. 33, 2012, p. 13-37.
-
Wang Z., Chen G. Analytical mode decomposition with Hilbert transform for modal parameter identification of buildings under ambient vibration. Engineering Structures, Vol. 59, 2013, p. 173-184.
-
Ceravolo R., Abbiati G. Time domain identification of structures: comparative analysis of output-only methods. Journal of Engineering Mechanics, Vol. 139, Issue 4, 2013, p. 537-544.
-
Lin C.-S., Chiang D.-Y. A modified random decrement technique for modal identification from nonstationary ambient response data only. Journal of Mechanical Science and Technology, Vol. 26, Issue 6, 2012, p. 1687-1696.
-
Ibrahim S. R., Mikulcik E. C. A method for the direct identification of vibration parameters from free response. Shock and Vibration Bulletin, Vol. 47, Issue 4, 1977, p. 183-198.
-
Lin C.-S., Tseng T.-C. Response-only modal identification using random decrement algorithm with time-varying threshold level. Journal of Mechanical Science and Technology, Vol. 28, Issue 6, 2014, p. 2099-2109.
-
Caicedo J. M. Practical guidelines for the Natural Excitation Technique (NExT) and the Eigensystem Realization Algorithm (ERA) for modal identification using ambient vibration. Experimental Techniques, Vol. 35, Issue 4, 2011, p. 52-58.
-
Juang J.-N., Pappa R. S. An eigensystem realization algorithm for modal parameter identification and model reduction. Journal of Guidance, Vol. 8, 1985, p. 620-627.
-
Zhou L. R., Yan G. R., Ou J. P. Response surface method based on radial basis functions for modeling large-scale structures in model updating. Computer-Aided Civil and Infrastructure Engineering, Vol. 28, Issue 3, 2013, p. 210-226.
-
Brownjohn J. M. W., Magalhaes F., Caetano E., Cunha A. Ambient vibration re-testing and operational modal analysis of the Humber Bridge. Engineering Structures, Vol. 32, 2010, p. 2003-2018.
-
Moser P., Moaveni B. Design and deployment of a continuous monitoring system for the Dowling Hall Footbridge. Experimental Techniques, Vol. 37, 2013, p. 15-26.
-
Jo H., Sim S.-H., Nagayama T., Spencer Jr. B. F. Development and application of high-sensitivity wireless smart sensors for decentralized stochastic modal identification. Journal of Engineering Mechanics, Vol. 138, Issue 6, 2012, p. 683-694.
-
Cimellaro G. P., Piantà S., De Stefano A. Output-only modal identification of Ancient L’Aquila City Hall and Civic Tower. Journal of Structural Engineering, Vol. 138, Issue 4, 2012, p. 481-491.
-
Wethyavivorn B., Surit S., Apichatyakul C., Lerdsivanon N. Model verification of Thai Historic Masonry Monuments. Journal of Performance of Constructed Facilities, Vol. 30, Issue 1, 2016, p. 4014188.
-
Dammika A. J., Kawarai K., Yamaguchi H., Matsumoto Y., Yoshioka T. Analytical damping evaluation complementary to experimental structural health monitoring of bridges. Journal of Bridge Engineering, Vol. 20, Issue 7, 2015, p. 4014095.
-
Chang M., Pakzad S. N. Modified natural excitation technique for stochastic modal identification. Journal of Bridge Engineering, Vol. 139, Issue 10, 2013, p. 1753-1762.
-
Van Overschee P., De Moor B. Subspace Identification for Linear Systems: Theory, Implementation, Applications. Kluwer Academic Publishers, Dordrecht, Netherlands, 1996.
-
Faurre P. L. Stochastic Realization Algorithms. System Identification: Advances and Case Studies, Academic Press, 1976.
-
Akaike H. Markovian representation of stochastic processes by canonical variables. SIAM Journal on Control, Vol. 13, Issue 1, 1975, p. 162-173.
-
Van Overschee P., De Moor B. Subspace algorithms for the stochastic identification problem. Automatica, Vol. 29, Issue 3, 1993, p. 649-660.
-
Peeters B., De Roeck G. Stochastic system identification for operational modal analysis: a review. Journal of Dynamic Systems, Measurement, and Control, Vol. 123, Issue 4, 2001, p. 659-667.
-
Ubertini F., Gentile C., Materazzi A. L. Automated modal identification in operational conditions and its application to bridges. Engineering Structures, Vol. 46, 2013, p. 264-278.
-
Bursi O. S., Kumar A., Abbiati G., Ceravolo R. Identification, model updating, and validation of a steel twin deck curved cable-stayed footbridge. Computer-Aided Civil and Infrastructure Engineering, Vol. 29, Issue 9, 2014, p. 703-722.
-
Shabbir F., Omenzetter P. Particle swarm optimization with sequential niche technique for dynamic finite element model updating. Computer-Aided Civil and Infrastructure Engineering, Vol. 30, Issue 5, 2015, p. 359-375.
-
Sevim B., Bayraktar A., Altunisik A. C, Atamtürktür S., Birinci F. Assessment of nonlinear seismic performance of a restored historical arch bridge using ambient vibrations. Nonlinear Dynamics, Vol. 63, Issue 4, 2011, p. 755-770.
-
Hu W.-H., Caetano E., Cunha A. Structural health monitoring of a stress-ribbon footbridge. Engineering Structures, Vol. 57, 2013, p. 578-593.
-
Cross E. J., Koo K. Y., Brownjohn J. M. W., Worden K. Long-term monitoring and data analysis of the Tamar Bridge. Mechanical Systems and Signal Processing, Vol. 35, 2013, p. 16-34.
-
Whelan M. J., Gangone M. V., Janoyan K. D., Jha R. Operational modal analysis of a multi-span skew bridge using real-time wireless sensor networks. Journal of Vibration and Control, Vol. 17, Issue 13, 2010, p. 1952-1963.
-
Foti D., Gattulli V., Potenza F. Output-only identification and model updating by dynamic testing in unfavorable conditions of a seismically damaged building. Computer-Aided Civil and Infrastructure Engineering, Vol. 29, Issue 9, 2014, p. 659-675.
-
Liu Y.-C., Loh C.-H., Ni Y.-Q. Stochastic subspace identification for output-only modal analysis: application to super high-rise tower under abnormal loading condition. Earthquake Engineering and Structural Dynamics, Vol. 42, 2013, p. 477-498.
-
Boscato G., Russo S., Ceravolo R., Fragonara L. Z. Global sensitivity-based model updating for heritage structures. Computer-Aided Civil and Infrastructure Engineering, Vol. 30, Issue 8, 2015, p. 620-635.
-
Li Z., Chang C. C. Tracking of structural dynamic characteristics using recursive stochastic subspace identification and instrumental variable technique. Journal of Engineering Mechanics, Vol. 138, Issue 6, 2012, p. 591-600.
-
Zhang G., Tang B., Tang G. An improved stochastic subspace identification for operational modal analysis. Measurement, Vol. 45, Issue 5, 2012, p. 1246-1256.
-
Hong A. L., Ubertini F., Betti R. New stochastic subspace approach for system identification and its application to long-span bridges. Journal of Engineering Mechanics, Vol. 139, Issue 6, 2013, p. 724-736.
-
Reynders E., Degrauwe D., De Roeck G., Magalhães F., Caetano E. Combined experimental-operational modal testing of footbridges. Journal of Engineering Mechanics, Vol. 136, Issue 6, 2010, p. 687-696.
-
Rathinam M., Petzold L. R. A new look at proper orthogonal decomposition. SIAM Journal on Numerical Analysis, Vol. 41, Issue 5, 2003, p. 1893-1925.
-
Kallinikidou E., Yun H.-B., Masri S. F., Caffrey J. P., Sheng L.-H. Application of orthogonal decomposition approaches to long-term monitoring of infrastructure systems. Journal of Engineering Mechanics, Vol. 139, Issue 6, 2013, p. 678-690.
-
Wang B.-T., Cheng D.-K. Modal analysis by free vibration response only for discrete and continuous systems. Journal of Sound and Vibration, Vol. 330, Issue 16, 2011, p. 3913-3929.
-
Oliveira C. S., Navarro M. Fundamental periods of vibration of RC buildings in Portugal from in-situ experimental and numerical techniques. Bulletin of Earthquake Engineering, Vol. 8, 2010, p. 609-642.
-
Hu X., Wang B., Ji H. Wireless sensor network-based structural health monitoring system for highway bridges. Computer-Aided Civil and Infrastructure Engineering, Vol. 28, Issue 3, 2013, p. 193-209.
-
Valla M., Gueguen P., Augère B., Goular D., Perrault M. Remote modal study of reinforced concrete buildings using a multipath lidar vibrometer. Journal of Structural Engineering, Vol. 141, Issue 1, 2015, p. D4014005.
-
Brincker R., Zhang L., Andersen P. Modal identification of output-only systems using frequency domain decomposition. Smart Materials and Structures, Vol. 10, Issue 3, 2001, p. 441-445.
-
Bendat J. S., Piersol A. G. Engineering Applications of Correlation and Spectral Analysis. Wiley, New York, 1993.
-
García-Palencia A. J., Santini-Bell E. A two-step model updating algorithm for parameter identification of linear elastic damped structures. Computer-Aided Civil and Infrastructure Engineering, Vol. 28, Issue 7, 2013, p. 509-521.
-
Erdogan H., Gülal E. Ambient vibration measurements of the Bosphorus suspension bridge by total station and GPS. Experimental Techniques, Vol. 37, Issue 3, 2013, p. 16-23.
-
Jacobsen N.-J., Andersen P., Brincker R. Using enhanced frequency domain decomposition as a robust technique to harmonic excitation in operational modal analysis. Proceedings of the International Conference on Noise and Vibration Engineering, September, Leuven, Belgium, 2006.
-
Gade S., Møller N. B, Herlufsen H., Konstantin-Hansen H. Frequency domain techniques for operational modal analysis. Proceedings of the 1st International Operational Modal Analysis Conference, Copenhagen, Denmark, 2005.
-
Altunisik A. C., Bayraktar A., Sevim B., Ates S. Ambient vibration based seismic evaluation of isolated Gülburnu Highway Bridge. Soil Dynamics and Earthquake Engineering, Vol. 31, Issue 11, 2011, p. 1496-1510.
-
Magalhães F., Cunha A., Caetano E., Brincker R. Damping estimation using free decays and ambient vibration tests. Mechanical Systems and Signal Processing, Vol. 24, Issue 5, 2010, p. 1274-1290.
-
Soyoz S., Taciroglu E., Orakcal K., Nigbor R., Skolnik D., Lus H., Safak E. Ambient and forced vibration testing of a reinforced concrete building before and after its seismic retrofitting. Journal of Structural Engineering, Vol. 139, 2013, p. 1741-1752.
-
Cismaşiu C., Narciso A., Amarante dos Santos F. Experimental dynamic characterization and finite-element updating of a footbridge structure. Journal of Performance of Constructed Facilities, Vol. 29, Issue 4, 2015, p. 4014116.
-
Wang T., Zhang L., Tamura Y. An operational modal analysis method in frequency and spatial domain. Earthquake Engineering and Engineering Vibration, Vol. 4, Issue 2, 2005, p. 295-300.
-
Agneni A., Crema L. B., Coppotelli G. Output-only analysis of structures with closely spaced poles. Mechanical Systems and Signal Processing, Vol. 24, Issue 5, 2010, p. 1240-1249.
-
Jiang X., Adeli H. Pseudospectra, MUSIC, and dynamic wavelet neural network for damage detection of highrise buildings. International Journal for Numerical Methods in Engineering, Vol. 71, 2007, p. 606-629.
-
Schmidt R. O. Multiple emitter location and signal parameter estimation. IEEE Transactions on Antennas Propagation, Vol. 34, Issue 3, 1986, p. 276-280.
-
Osornio-Rios R. A., Amezquita-Sanchez J. P., Romero-Troncoso R. J., Garcia-Perez A. MUSIC-ANN Analysis for locating structural damages in a truss-type structure by means of vibrations. Computer-Aided Civil and Infrastructure Engineering, Vol. 27, Issue 9, 2012, p. 687-698.
-
Amezquita-Sanchez J. P., Garcia-Perez A., Romero-Troncoso R. J., Osornio-Rios R. A., Herrera-Ruiz G. High-resolution spectral-analysis for identifying the natural modes of a truss-type structure by means of vibrations. Journal of Vibration and Control, Vol. 19, Issue 16, 2013, p. 2347-2356.
-
Perez-Ramirez C. A., Amezquita-Sanchez J. P., Adeli H., Valtierra-Rodriguez M., Camarena-Martinez D., Romero-Troncoso R. J. New methodology for modal parameters identification of smart civil structures using ambient vibrations and synchrosqueezed wavelet transform. Engineering Applications of Artificial Intelligence, Vol. 48, 2016, p. 1-12.
-
Ghodrati Amiri G., Abdolahi Rad A., Khanmohamadi Hazaveh N. Wavelet based method for generating non-stationary artificial pulse-like near-fault ground motions. Computer-Aided Civil and Infrastructure Engineering, Vol. 29, Issue 10, 2014, p. 758-770.
-
Perez G., Conci A., Moreno A. B., Hernandez-Tamames J. A. Rician noise attenuation in the wavelet packet transformed domain for brain MRI. Integrated Computer-Aided Engineering, Vol. 21, Issue 2, 2014, p. 163-175.
-
Adeli H., Kim H. Wavelet-hybrid feedback-least mean square algorithm for robust control of structures. Journal of Structural Engineering, Vol. 130, Issue 1, 2004, p. 128-137.
-
Kim H., Adeli H. Hybrid feedback-least mean square algorithm for structural control. Journal of Structural Engineering, Vol. 130, Issue 1, 2004, p. 120-127.
-
Amini F., Zabihi-Samani M. A wavelet-based adaptive pole assignment method for structural control. Computer-Aided Civil and Infrastructure Engineering, Vol. 29, Issue 6, 2014, p. 464-477.
-
Dai H., Wang W. An adaptive wavelet frame neural network method for efficient reliability analysis. Computer-Aided Civil and Infrastructure Engineering, Vol. 29, Issue 10, 2014, p. 801-814.
-
Dai H., Wang W., Zhang H. A multiwavelet neural network-based response surface method for structural reliability analysis. Computer-Aided Civil and Infrastructure Engineering, Vol. 30, Issue 2, 2015, p. 151-162.
-
Katicha S. W., Flintsch G., Ferne B., Bryce J. Wavelet denoising of TSD deflection slope measurements for improved pavement structural evaluation. Computer-Aided Civil and Infrastructure Engineering, Vol. 29, Issue 6, 2014, p. 399-415.
-
Adeli H., Jiang X. Intelligent Infrastructure: Neural Networks, Wavelets, and Chaos Theory for Intelligent Transportation Systems and Smart Structures. CRC Press, Boca Raton, 2009.
-
Vahabi Z., Amirfattahi R., Ghassemi F., Shayegh F. Online epileptic seizure prediction using wavelet-based Bi-phase correlation of electrical signal tomography. International Journal of Neural Systems, Vol. 25, Issue 6, 2015, p. 1550028.
-
Hsu W. Y. Assembling a multi-feature EEG classifier for left-right motor data using wavelet-based fuzzy approximate entropy for improved accuracy. International Journal of Neural Systems, Vol. 25, Issue 8, 2015, p. 1550037.
-
Ortiz-Rosario A., Adeli H., Buford J. A. Wavelet methodology to improve single unit isolation in primary motor cortex cells. Journal of Neuroscience Methods, Vol. 246, 2015, p. 106-118.
-
Ülker-Kaustell M., Karoumi R. Application of the continuous wavelet transform on the free vibrations of a steel-concrete composite railway bridge. Engineering Structures, Vol. 33, Issue 3, 2011, p. 911-919.
-
Le T.-P., Paultrec P. Modal identification based on continuous wavelet transform and ambient excitation tests. Journal of Sound and Vibration, Vol. 331, Issue 9, 2012, p. 2023-2037.
-
Kim Y. S., Chen L.-Q. Separation of closely spaced modes by combining complex envelope displacement analysis with method of generating intrinsic mode functions through filtering algorithm based on wavelet packet decomposition. Applied Mathematics and Mechanics, Vol. 34, Issue 7, 2013, p. 801-810.
-
Holschneider M., Kronland-Martinet R., Morlet J., Tchamitchian P. A real-time algorithm for signal analysis with the help of the wavelet transform. Wavelets, Springer Berlin Heidelberg, 1989, p. 286-297.
-
Pesquet J.-C., Krim H., Carfantan H. Time-invariant orthonormal wavelet representations. IEEE Transactions on Signal Processing, Vol. 44, Issue 8, 1996, p. 1964-1970.
-
Sadhu A., Hazra B., Narasimhan S. Decentralized modal identification of structures using parallel factor decomposition and sparse blind source separation. Mechanical Systems and Signal Processing, Vol. 41, Issues 1-2, 2013, p. 396-419.
-
Su W. C., Huang C. S., Chen C. H., Liu C. Y., Huang H. C., Le Q. T. Identifying the modal parameters of a structure from ambient vibration data via the stationary wavelet packet. Computer-Aided Civil and Infrastructure Engineering, Vol. 29, Issue 10, 2014, p. 738-757.
-
Daubechies I., Lu J., Wu H. T. Synchrosqueezed wavelet transforms: An empirical mode decomposition-like tool. Applied and Computational Harmonic Analysis, Vol. 30, Issue 2, 2011, p. 243-261.
-
Huang N. E., Shen Z., Long S. R., Wu M. C., Shih H. H., Zheng Q., Yen N.-C., Tung C. C., Liu H. M. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis. Proceedings of the Royal Society of London A: Mathematical, Physical and Engineering Sciences, Vol. 454, Issue 1971, 1998, p. 903-995.
-
Yan B., Miyamoto A. A comparative study of modal parameter identification based on wavelet and Hilbert-Huang transforms. Computer-Aided Civil and Infrastructure Engineering, Vol. 21, Issue 1, 2006, p. 9-23.
-
Zhao Z., Wang Y. Analysis of diastolic murmurs for coronary artery disease-based on Hilbert Huang transform. IEEE International Conference on Machine Learning and Cybernetics, Hong Kong, China, Vol. 6, 2007, p. 3337-3342.
-
Antonino-Daviu J. A., Riera-Guasp M., Pineda-Sanchez M., Perez R. B. A critical comparison between DWT and Hilbert-Huang-based methods for the diagnosis of rotor bar failures in induction machines. IEEE Transaction on Industrial Applications, Vol. 45, Issue 5, 2009, p. 1794-1803.
-
Chen C. H., Wang C. H., Lui J. Y., Lui C., Liang W. T., Yen H. Y., Yeh Y. H., Chia Y. P., Wang Y. Identification of earthquakes signals from groundwater level records using the HHT method. Geophysical Journal International, Vol. 180, 2010, p. 1231-1241.
-
Shi W., Shan J., Lu X. Modal identification of Shanghai World Financial Center both from free and ambient vibration response. Engineering Structures, Vol. 34, 2012, p. 14-26.
-
Ditommaso R., Mucciarelli M., Parolai S., Picozzi M. Monitoring the structural dynamic response of a Masonry Tower: comparing classical and time-frequency analyses. Bulletin of Earthquake Engineering, Vol. 10, Issue 4, 2012, p. 1221-1235.
-
Wu Z., Huang N. Ensemble empirical mode decomposition: a noise-assisted data analysis method. Advances in Adaptive Data Analysis, Vol. 1, Issue 1, 2009, p. 1-41.
-
Pai P. F., Nguyen B.-A., Sundaresan M. H. Nonlinearity identification by time-domain-only signal processing. International Journal of Non-Linear Mechanics, Vol. 54, 2013, p. 85-98.
-
Luengo D., Monzon S., Triganoz T., Via J., Artes-Rodrıguez A. Blind analysis of atrial fibrillation electrograms: a sparsity-aware formulation. Integrated Computer-Aided Engineering, Vol. 22, Issue 1, 2015, p. 71-85.
-
Hyvarinen A., Karhunen J., Oja E. Independent Component Analysis. John Wiley, New York, 2001.
-
Belouchrani A., Abed-Meraim K., Cardoso J. Moulines E. A blind source separation technique using second-order statistics. IEEE Transactions on Signal Processing, Vol. 45, Issue 2, 1997, p. 434-444.
-
Poncelet F., Kerschen G., Golinval J.-C., Verhelstb D. Output-only modal analysis using blind source separation techniques. Mechanical Systems and Signal Processing, Vol. 21, Issue 6, 2007, p. 2335-2358.
-
Hazra B., Sadhu A., Roffel A. J., Narasimhan S. Hybrid time-frequency blind source separation towards ambient system identification of structures. Journal of Engineering Mechanics, Vol. 27, Issue 5, 2012, p. 314-332.
-
Yang K., Yu K., Li Q. Modal parameter extraction based on Hilbert transform and complex independent component analysis with reference. Mechanical Systems and Signal Processing, Vol. 40, 2013, p. 257-268.
-
Cara F. J., Carpio J., Juan J., Alarcón E. An approach to operational modal analysis using the expectation maximization algorithm. Mechanical Systems and Signal Processing, Vol. 31, 2012, p. 109-129.
-
Cheung S. H., Beck J. L. Calculation of posterior probabilities for Bayesian model class assessment and averaging from posterior samples based on dynamic system data. Computer-Aided Civil and Infrastructure Engineering, Vol. 25, Issue 5, 2010, p. 304-321.
-
Au S. K. Fast Bayesian FFT method for ambient modal identification with separated modes. Journal of Engineering Mechanics, Vol. 137, Issue 3, 2011, p. 214-226.
-
Yan W.-J., Katafygiotis L. S. A two-stage fast Bayesian spectral density approach for ambient modal analysis. Part I: posterior most probable value and uncertainty. Mechanical Systems and Signal Processing, Vol. 54, Issue 55, 2015, p. 39-55.
-
Zheng J., Cheng J., Yang Y. A rolling bearing fault diagnosis approach based on LCD and fuzzy entropy. Mechanism and Machine Theory, Vol. 70, 2013, p. 441-453.
-
Chu P. C., Fan C., Huang N. E. Compact Empirical mode decomposition: an algorithm to reduce mode mixing, end effect, and detrend uncertainty. Advances in Adaptive Data Analysis, Vol. 4, Issue 3, 2012, p. 1250017.
-
Amezquita-Sanchez J. P., Adeli H. A new music-empirical wavelet transform methodology for time-frequency analysis of noisy nonlinear and non-stationary signals. Digital Signal Processing, Vol. 45, 2014, p. 55-68.
-
Chui C. K., Mhaskar H. N. Signal decomposition and analysis via extraction of frequencies. Applied and Computational Harmonic Analysis, Vol. 40, Issue 1, 2016, p. 97-136.
About this article
This work was partially supported by the Mexican Council of Science and Technology (CONACyT) by the scholarship 289377.
This article is the result of a collaborative research project initiated during 2013-2014 when Juan Pablo Amezquita-Sanchez was a PostDoctoral Visiting Scholar under the supervision of Hojjat Adeli at The Ohio State University. Carlos Andres Perez-Ramirez and Juan Pablo Amezquita-Sanchez prepared the first draft of the manuscript and investigated the main time-frequency algorithms employed in MPI, as well as their advantages and disadvantages. Martin Valtierra-Rodriguez investigated the techniques employed for exciting a civil structure and their strengths and weaknesses. Aurelio Dominguez-Gonzalez examined the algorithms used for compensating the temperature effect in the MPI and their advantages and disadvantages. Rene de Jesus Romero-Troncoso and Roque Alfredo Osornio-Rios revised and investigated new algorithms with potential to be employed in the MPI. Hojjat Adeli guided the research, provided the knowledge of MPI, and revised the article critically for important intellectual content.
