Abstract
The present of goal investigation is to study the effect of 2D linearly varying temperature on the vibrations of non-homogeneous trapezoidal plate whose thickness also varies linearly in both directions and density varies linearly in one direction. Boundary condition which is C-S-C-S with two term deflection is taken into consideration. Rayleigh-Ritz method is used to find the solution of the problem. The effect of other plate parameters such as non-homogeneity constant, taper constant and aspect ratios have also been studied. Results are calculated with accuracy and presented in tabular graphical form.
1. Introduction
Plate theory has been applied to reduce vibration and noise in structures since the end of the 19th century where it began with the work of German physicist Chladni, who discovered various modes of free vibrations experimentally.
Since then, it has developed into an escalating and expansive field with a wide variety of theoretical and empirical techniques, dealing with increasingly complicated problems. In marine and aerospace engineering fields, where lightweight structural elements with orthotropic materials are of primary importance, orthotropic trapezoidal plate has extensive application. They are essentially thin plate structures which provide enhanced stiffness and stability characteristics. Hey also have widespread application in many other branches of modern civil, mechanical and structural engineering and, in these applications, they are regularly subjected to static and time varying loads. Hence, analysis of orthotropic trapezoidal plate under different conditions has always been an area of immense interest to researchers. Research work on the dynamic characteristics of orthotropic trapezoidal plate has a long history as different researchers have employed different methodologies to perform dynamic analysis of such structures.
Plates of variable thickness are used in nuclear reactor structures, naval structures, and aeronautical fields, electro mechanical transducers for the electronic telephones and mirrors and lenses in optical system. he practical importance of these plates has made vibration analysis essential for avoiding resonance excited by internal or external forces.
Also, in recent years, the development of solid propellant rocket motors and the increased use of sot filaments in aerospace structure and high speed runways, many practical solid structure interaction problems such as floor slabs of multistory buildings and buildings activities in cold regions have intensified the need for solution of various problems of plates and other structures supported on elastic media.
Vibrational effect is not only restricted in the field of engineering and science but, our daily life is also affected by it. There are many authors who deal in the study of vibration phenomena of plates by considering different kind of shapes, varying thickness, homogeneity or non-homogeneity, with or without consideration of temperature effect.
Many authors have reported about the vibrational analysis of different types of plates. Some of them are mentioned here.
Zenkour [1] studied an exact solution for bending thin rectangular plates with uniform, linear, and quadratic thickness variations. Tomar et al. [2] attempted a problem of axisymmetric vibrations of an isotropic elastic non-homogeneous circular plate of linearly varying thickness. Tomar et al. [3] studied features of the free vibration of an isotropic non-homogeneous infinite plate of parabolically varying thickness. Srinivas et al. [4] did an exact analysis for vibration of simply supported homogeneous and laminated thick rectangular plates. Saliba [5] considered fully clamped symmetrical trapezoidal plates with free transverse vibration.
The finite element method of the vibration of trapezoidal plates is discussed by Orris and Petyt [6]. Qatu [7] studied the natural frequencies for cantilevered laminated composite right triangular and trapezoidal plates. Kitipornchai et al. [8] discussed the problem of vibrations of thick trapezoidal plates.
Recently, Gupta and Sharma [9] studied the thermal effect on free vibration of orthotropic thin trapezoidal plate of linearly varying thickness. The authors have so far not come across any paper dealing with bi- linearly varying temperature, thickness and linearly varying density. In the present work, the effect of non-homogeneity, taper constant, thermal gradient and aspect ratios has been studied. The frequencies for the first two modes of vibration are obtained for C-S-C-S non-homogeneous trapezoidal plate by Rayleigh-Ritz method and display in the form of graphs.
2. Geometry of the plate
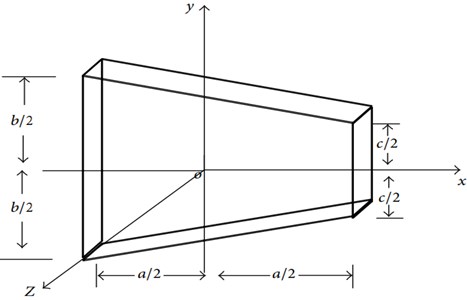
The plate which is used for this paper is shown in Fig. 1. This is thin, symmetric and non-homogeneous trapezoidal plate. At the left edge, maximum occurring thickness is and at the right, minimum occurring thickness is .
Fig. 1Variable varying thickness of trapezoidal plate
3. Methodology and equation of motion
Consider atrapezoidal plate with bi-linearly varying thickness in both and directions taken as:
where is thickness along and .
Non-homogeneity of plate arises due to linear variation in density along -axis as:
Two-dimensional temperature distribution 𝜏 along the length for trapezoidal plate under consideration is:
where denotes the temperature excess above the reference and denotes the temperature excess above the reference temperature.
Modulus of elasticity for elastic materials, is described as:
where is the value of Young’s modulus along the reference temperature i.e. at and is the slope of the variation of and .
On substituting value of from Eq. (3) into (4):
where .
4. Equation of motion
The governing differential equation for kinetic energy and strain energy is given by:
Flexural rigidity of the plate is:
Also:
is the plate’s flexural rigidity at the side , A is the area of the plate and is the mass density per unit area of the plate.
Using Eqs. (9) and (5) in (8) flexural rigidity is given by:
Using Eq. (10) in (7) and (1), (2) in (6):
5. Deflection function and boundary condition
A two term deflection function is taken as:
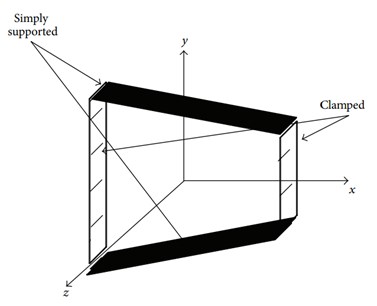
where and are constants to be evaluated. Eq. (13) satisfies boundary conditions and provides good frequency estimation. Clamped-Simply supported-Clamped-Simply supported plate is taken into consideration as shown in Fig. 2.
Fig. 2Boundary conditions for the plate
Also, considered plate having boundaries which is defined a:
6. Method of solution
For finding the solution, Rayleigh-Ritz technique is used. According to its maximum strain energy must be equal to maximum kinetic energy, so for the problem under consideration we have:
Using Eq. (14) in (11) and (12):
Now Eq. (15) becomes:
where:
and is a frequency parameter.
Two unknown and are involve in Eq. (18) because of substitution of from Eq (13). These two unknowns are to be evaluated from Eq. (18), as follows:
On simplifying Eq. (21), we get:
where , involve parametric constant and the frequency parameter.
For non-zero solution, the determinant of the coefficient of Eq. (22) must vanish. Therefore, the equation of frequency becomes:
After solving Eq. (23), we get quadratic equation in .
7. Result and discussion
Here numerical results for a non-homogenous trapezoidal plate of bi-linearly varying thickness are calculated. Frequencies are calculated for the first two modes of vibration for different values of taper constant and thermal gradient, for C-S-C-S boundary condition.
Frequency Eq. (23) is quadratic in , so we have tworoots. First two vibrational modes of frequency are calculated for a C-S-C-S, trapezoidal plate, for various values of , , , , and 0.33 along with linearly varying thickness. Graphical representations are used for the results.
In Fig. 3 it is observed that the frequency parameter increases with increasing values of thermal gradient for different values of taper constant (4.0, 0.0), non-homogeneity constant (0.4, 1.0) and aspect ratios ( 1.0), (0.5) for both the modes of vibration. The rate of increase as well as the value of frequency parameter is higher in second mode in comparison to the first mode.
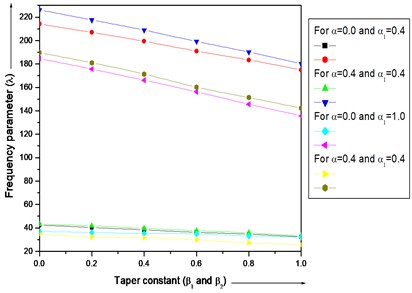
In Fig. 4 it is seen that frequency parameter decreases with increasing values of taper constants ( and ), for different values of thermal gradient (0.0, 0.4), taper constants ( and ), non-homogeneity constant (0.4, 1.0) and aspect ratios ( 1.0), (0.5) for both the modes of vibration. The rate of decrease as well as the value of frequency parameter is higher in second mode in comparison to the first mode.
Fig. 3Frequency parameter (λ) for a trapezoidal plate for different values of taper constant (β1=β2= 4.0, 0.0), thermal gradient (α), non-homogeneity constant (α1= 0.4, 1.0) and aspect ratios (a/b= 1.0), (c/b= 0.5)
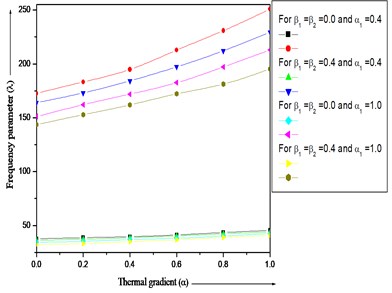
Fig. 4Frequency parameter (λ) for a trapezoidal plate for different values of thermal gradient (α= 0.0, 0.4), taper constant (β1 and β2), non-homogeneity constant (α1= 0.4, 1.0) and aspect ratios (a/b= 1.0), (c/b= 0.5)
From Fig. 5 and 6 it is noticed that the frequency parameter decreases with increasing values of aspect ratio and for different combinations of thermal gradient ( and ), taper constant () and fixed value of non-homogeneity constant ( 0.0) and aspect ratio ( 0.75) for both the modes of vibration. The rate of decrease of frequency parameter in Fig. 5 is higher in first and second mode in comparison
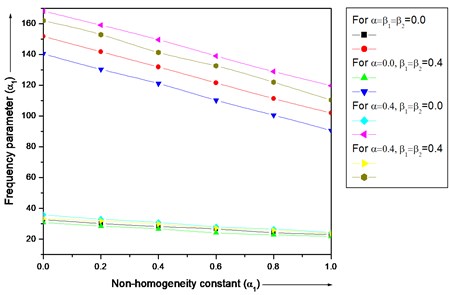
Fig. 7 clearly shows that frequency parameter decreases with increasing value of non-homogeneity constant for different value of non-homogeneity constant () with different combinations of thermal gradient ( and ), and taper constant () and aspect ratios ( 1.0), ( 1.0) for both the mode of vibration.
Fig. 5Frequency parameter (λ) for a trapezoidal plate for different combinations of thermal gradient (β1 and β2), taper constant (α) and fixed value of non-homogeneity constant (α1= 0.0) and aspect ratio (c/b= 0.75)
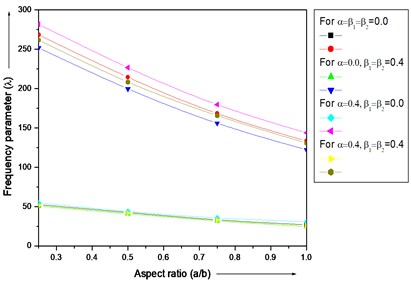
Fig. 6Frequency parameter (λ) for a trapezoidal plate for different combinations of thermal gradient (β1 and β2), taper constant (α) and fixed value of non-homogeneity constant (α1= 0.0) and aspect ratio (a/b= 0.75)
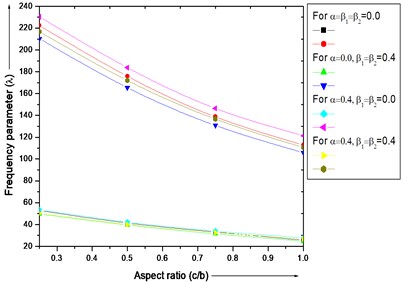
Fig. 7Frequency parameter (λ) for a trapezoidal plate for different value of non-homogeneity constant (α1) with different combinations of thermal gradient (β1 and β2) and taper constant (α) and aspect ratios (a/b= 1.0), (c/b= 1.0)
8. Conclusions
Our main aim is to provide such kind of a mathematical design so that scientist can perceive their potential in mechanical engineering field and increase strength, durability and efficiency of mechanical design and structuring with a practical approach. Actually, this is the need of the hour to develop more but authentic mathematical model for the help of mechanical engineers. Therefore, mechanical engineers and technocrats are advised to study and get the practical importance of the present paper and to provide much better structure and machines with more safety and economy.
References
-
Zenkour A. M. An exact solution for the bending of thin rectangular plates with uniform, linear, and quadratic thickness variations. International Journal of Mechanical Sciences, Vol. 45, Issue 2, 2003, p. 295-315.
-
Tomar J. S., Gupta D. C., Jain N. C. Axisymmetric vibrations of an isotropic elastic non-homogeneous circular plate of linearly varying thickness. Journal of Sound and Vibration, Vol. 85, Issue 3, 1982, p. 365-370.
-
Tomar J. S., Gupta D. C., Jain N. C. Free vibrations of anisotropic non-homogeneous infinite plate of parabolically varying thickness. International Journal of Pure and Applied Mathematics, Vol. 15, Issue 2, 1984, p. 220-221.
-
Srinivas S., Joga Rao C. V., Rao A. K. An exact analysis for vibration of simply-supported homogeneous and laminated thick rectangular plates. Journal of Sound and Vibration, Vol. 12, Issue 2, 1970, p. 187-199.
-
Saliba H. T. Transverse free vibration of fully clamped symmetrical trapezoidal plates. Journal of Sound and Vibration, Vol. 126, Issue 2, 1988, p. 237-247.
-
Orrisand R. M., Petyt M. A finite element study of the vibration of trapezoidal plates. Journal of Sound and Vibration, Vol. 27, Issue 3, 1973, p. 325-344.
-
Qatu M. S. Natural frequencies for cantilevered laminated composite right triangular and trapezoidal plates. Composites Science and Technology, Vol. 51, Issue 3, 1994, p. 441-449.
-
Kitipornchai S., Xiang Y., Liew K. M., Lim M. K. A global approach for vibration of thick trapezoidal plates. Computers and Structures, Vol. 53, Issue 1, 1994, p. 83-92.
-
Gupta A. K., Sharma S. Thermally induced vibration of orthotropic trapezoidal plate of linearly varying thickness. Journal of Vibration and Control, Vol. 17, Issue 10, 2011, p. 1591-1598.
-
Khanna A., Sharma A. K. A computational prediction on vibration of square plate by varying thickness with bi-dimensional thermal effect. International Journal of Emerging in Engineering and Development, Vol. 2, Issue 3, 2012, p. 191-196.
-
Khanna A., Sharma A. K. Effect of thermal gradient on vibration of visco-elastic plate with thickness variation. American Journal of Computational and Applied Mathematics, Vol. 2, Issue 1, 2012, p. 34-36.
-
Khanna A., Sharma A. K. Mechanical vibration of visco-elastic plate with thickness variation. International Journal of Applied Mathematical Research, Vol. 1, Issue 2, 2012, p. 150-158.
-
Khanna A., Kaur N., Sharma A. K. Effect of varying Poisson ratio on thermally induced vibrations of non-homogeneous rectangular plate. Indian Journal of Science and Technology, Vol. 5, Issue 9, 2012, p. 3263-3267.
-
Khanna A., Sharma A. K. Analysis of free vibrations of VISCO elastic square plate of variable thickness with temperature effect. International Journal of Applied Engineering Research, Vol. 2, Issue 2, 2011, p. 312-317.
-
Sharma Subodh Kumar, Sharma Ashish Kumar Rayleigh‑Ritz method for analyzing free vibration of orthotropic rectangular plate with 2D thickness and temperature variation. Journal of Vibroengineering, Vol. 17, Issue 4, 2015, p. 1989-2000.
-
Sharma Subodh Kumar, Sharma Ashish Kumar Mathematically study on vibration of visco‑elastic parallelogram plate. Mathematical Models in Engineering, Vol. 1, Issue 1, 2015, p. 12-19.
